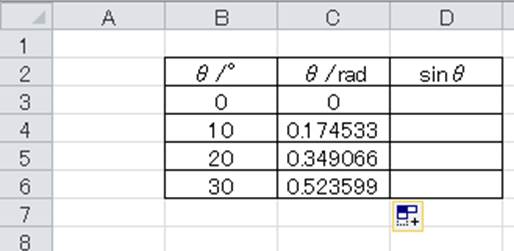
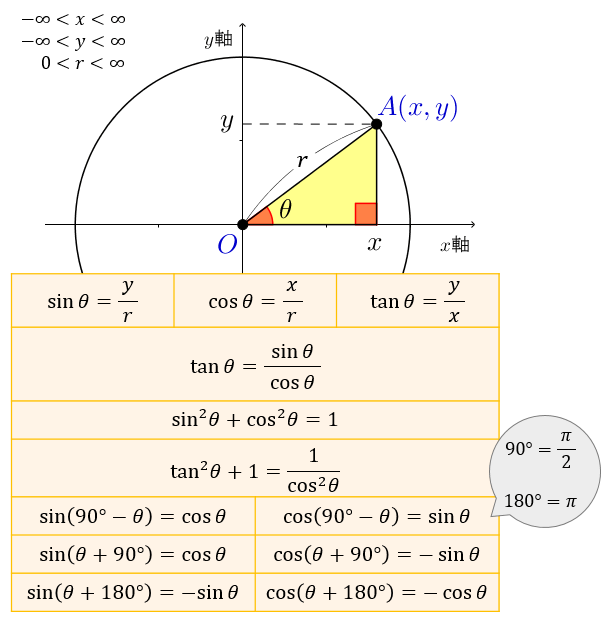
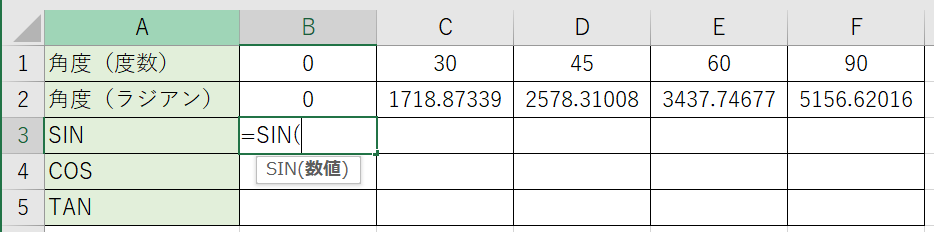
29/6/17 最後に、三角関数の公式の中でも特によく使う4つの式を紹介します。 1つ目は tanθ = sinθ / cosθ 。 これは、 sinθ, cosθ, tanθ の定義式から求められます。 2つ目は sin2θ cos2θ = 1 。補角の公式: sin ( 18 0 ∘ − θ) = sin θ \sin (180^ {\circ}\theta)=\sin\theta sin(180∘ −θ) = sinθ cos ( 18 0 ∘ − θ) = − cos θ \cos (180^ {\circ}\theta)=\cos\theta cos(180∘ −θ) = −cosθ tan ( 18 0 ∘ − θ) = − tan θ \tan (180^ {\circ}\theta)=\tan\theta tan(180∘ −θ) = −tanθ角度が30度の場合のcos,sin,tanを求めてみましょう。 度数を直接使うには、RADINA関数を使ってラジアンに直して計算します。 sin,cosカーブを書いてみます セルに「0」と入力します。
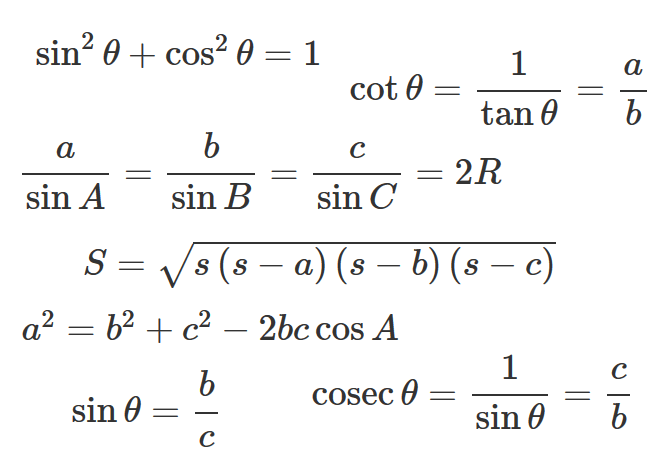
電気数学のお勉強 三角関数
Sin cos 変換表
Sin cos 変換表-Sin( ) sin( ) ( sin sin cos sin ) ³ S S 2 0 ( ) sin( ) 1 an f x mx dx 同様に、cos(mx)をかけて積分すると ³ S S 2 0 ( ) cos( ) 1 bn f x mx dx ※ sin(nx)cos(mx) の積分は、sin が奇関数、cos が遇関数なのでゼロになる。 sin(nx)sin(mx) , cos(nx)cos(mx)の積分は、積和変換でcos になるためゼロだが、n=m三角関数は sin や cos など英記号で表すので難しいと思っている人が意外に多いが、正弦波交流を取り扱う上で重要な関数である。 ここでは、三角関数のグラフと交流の瞬時値の式を対比させ交流波形を描くこと、瞬時値の式から位相の進み遅れが分かることを目標に解説する。




1995 号 ディジタル三角関数発生回路 Astamuse
244 第9 章 行列と線形変換 前のxx で議論した,点やベクトルを角 だけ回転する変換f については, x′ y′ = f x y) = (xcos ysin xsin ycos ) = (cos sin sin cos )(x y) となるので,f の表現行列は cos sin sin cos ) です.この回転を表す1 次変換f はしばしば利用されるので,その表現行列をR と略記しましょうCOS 関数の書式に /180 を掛けるか、または RADIANS 関数を使用して角度をラジアンに変換します。 使用例 次の表のサンプル データをコピーし、新しい Excel ワークシートのセル A1 に貼り付けます。Def encode (df, col) # この方法だと場合によって最大値が変化するデータでは正確な値は出ない # 例:月の日数が30日や31日の場合がある df col '_cos' = np cos (2 * np pi * df col / df col max ()) df col '_sin' = np sin (2 * np pi * df col / df col max ()) return df df = encode (df, 'dow') df = encode (df, 'hour') df = encode (df, 'day') df = encode (df, 'month')
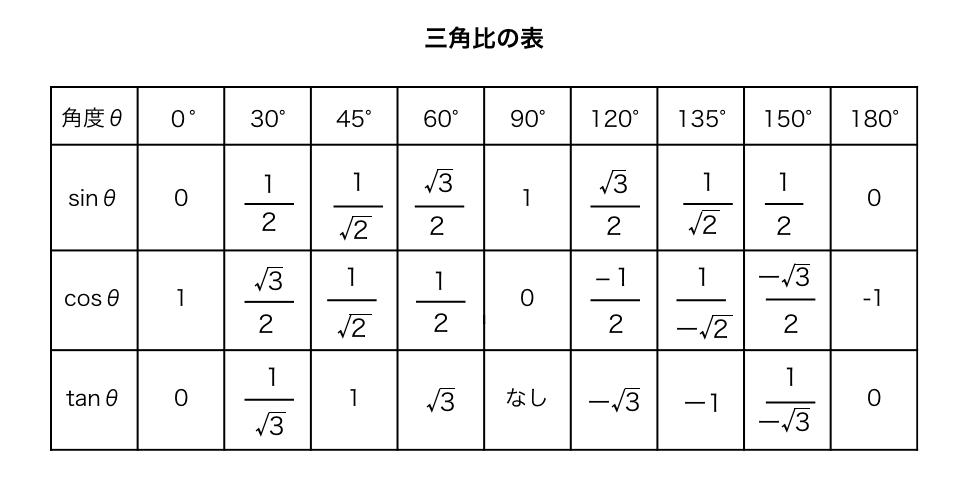
0 0 1 0 1 2 3 4 5 6 7 8Sin (サイン) 、cos (コサイン) 、tan (タンジェント) を知らなくても解ける! 高卒認定(高認)試験の数学の第6問で三角比の計算はよく出題されます。この問題は三角比のことをよく知らなくても、次の表を覚えれば解けてしまいます。1 2 cos sin − − − − = z z z ω ω なんだか難しいそうで嫌になった人もいるかもしれない。しかし実は,z変換は,とても簡単で,しかも役に立つもの なのだ。次回の「z変換の性質」で理解できるはず・・・。 { } 1 1 1 − − = e z Z e a an
1/3/21 同様に であるため、 ポイント こうした様々な三角比の足し算引き算は、ほぼ確実にシンプルな答えになります。 180º θ の三角比などを思い出して、一つ一つ丁寧に式変形していきましょう。 途中で符号や sin, cos のミスがあると途端に複雑になってしまいます。 逆に、複雑な結果になってしまったら「どこかで計算ミスをしていないかな? 」と自分で表記 逆三角関数に対して用いられる表記はたくさんある。 sin −1 (x), cos −1 (x), tan −1 (x) などの表記はしばしば使われるが、この慣習は関数の合成ではなく冪乗を意味する sin 2 (x) のような表現の一般的なセマンティクスと論理的には相反し、それゆえ乗法逆元と合成的逆の間の混乱を起こすラプラス変換表 cosh at at a sinh 1 cosat at a sin 1 t u(t) δ(t) s2 a2 s ζω ω ζω sin 1 1 cos 2 a



三角関数の真数表 技術情報 Misumi Vona ミスミ




三角関数 Sin Cos Tanの表について 写真の表って全部覚える必要ありま 数学 教えて Goo
902 filas 三角関数表 この三角関数表には、01° ごとの角度(度数)に対する、サイン(sin)、コサイン(cos)、 タンジェント(tan) 、および角度の ラジアン(rad) の値が小数第4位まで掲載されています。 デフォルトでは 1° 単位の値しか表示されていませんので、01° 単位で表示したい場合は、 詳しく知りたい度数の行をクリック してください。 行が展開しますSin 2 θ cos 2 θ = 1 1 tan 2 θ = cec 2 θ 1 cot 2 θ = cosec 2 θ tanθ = sinθ/cosθ cotθ = cosθ/sinθ sin2θ = 2sinθcosθ cos2θ = cos 2 θ sin 2 θ tan2θ = 2tanθ/(1 tan 2 θ)1 filas sin cos tan;



数学 三角関数 Abs Pi Sinなど の使い方 Excel関数



三角関数表 Pukiwiki
1 a ⋅ sinc ( ξ a ) {\displaystyle {\frac {1} {a}}\cdot \operatorname {sinc} \left ( {\frac {\xi } {a}}\right)} 1 2 π a 2 ⋅ sinc ( ω 2 π a ) {\displaystyle {\frac {1} {\sqrt {2\pi a^ {2}}}}\cdot \operatorname {sinc} \left ( {\frac {\omega } {2\pi a}}\right)}Sin(数値) sin 関数の書式には、次の引数があります。 数値 必ず指定します。 サインを求める角度をラジアンで指定します。 解説 指定する角度の単位が度である場合は、pi()/180 を掛けるか、radians 関数を使用してラジアンに変換してください。 使用例8/8/15 sin (ωt)とcos (ωt)のLaplace変換 制御システムの設計に役に立つLaplace変換ですが,普段は 変換表 を見て時間世界とs世界を行ったり来たりするだけです ここでは表を使わずに \cos (\omega t) cos(ωt) のLaplace変換を行います 変換をするにあたり知っておきたい予備




Excelの三角関数 Sin Cos Tan の具体的な使い方と注意点 サインコサインタンジェント わえなび ワード エクセル問題集




高校数学 三角関数の3倍角の公式の証明とゴロ合わせ 受験の月
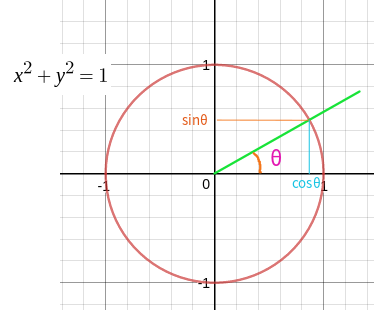
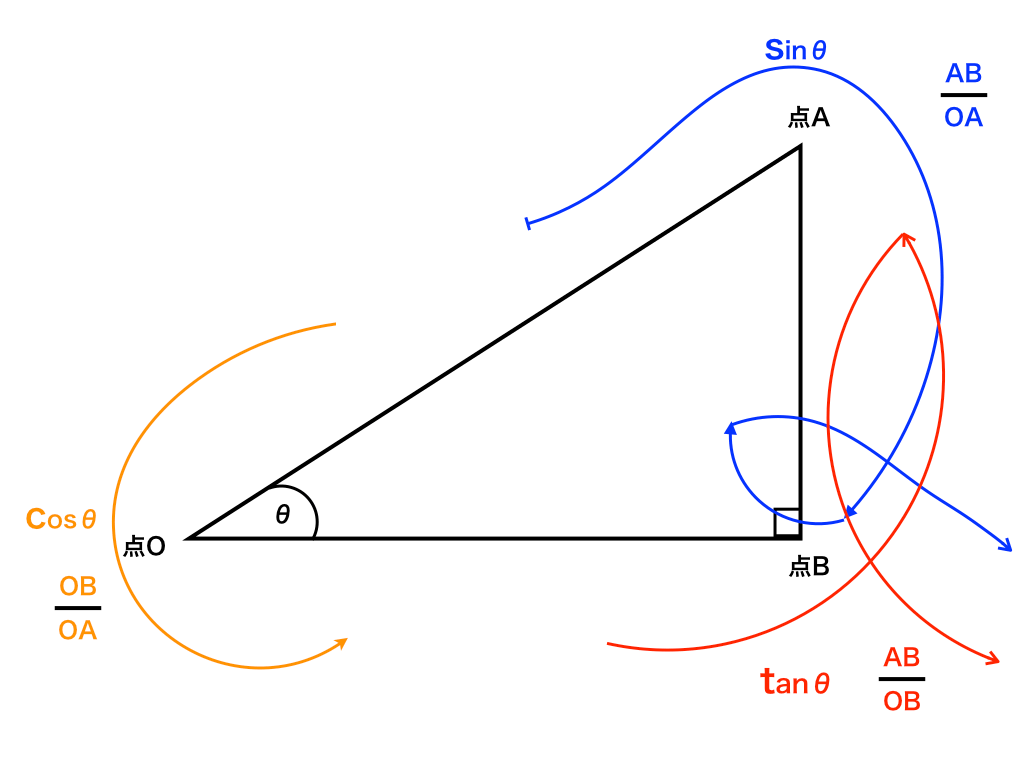
三角比の表・三角関数表(sin cos tan の値)の一覧! 21年2月19日 この記事では、「三角比の表」と「三角関数表」を徹底解説していきます。 (サイン コサイン タンジェント)の主要な値を度数・ラジアンの両方で紹介しますので、この記事を通して覚えラプラス変換は、元はといえば線形微分方程式を解くテクニックとして発達し、後から理論体系が ラプラス変換の結果を直接利用するの ではなく、変換して問題を解き、その答を逆変換で元の世界に引き戻すという使い方が主である。 (解法) (i) 𝑓 19/4/18 三角関数で角度から座標を定めるふたつの方程式 まずは、ふたつの方程式を以下に示しましょう。 第1は、原点 ( 0, 0) からの距離 r と x 軸正方向となす角度 θ から座標 ( x, y) を求めます。 x = r cos θ y = r sin θ 第2は、座標 ( x, y) を原点 ( 0, 0) から



三角関数の公式




Sin Cos Tan 表
三角関数のラプラス変換 \cos \omega t cosωt のラプラス変換は次の通りです。 これは覚えてしまった方がなにかと便利です。 が、忘れてしまっても簡単に導けます。 試しに \cos \omega t cosωt のラプラス変換を計算してみましょう。 まず、 オイラーの公式例題4 三角関数 f (t) = sin (ωt) のラプラス変換 例題3 と同様に ω を正の実数として, 三角関数 f (t) = sin (ωt) の ラプラス変換 を求めます. オイラーの公式 から得られる2式に減算を適用し, 2 j で割ると, が得られます.これより, cos の場合と同様にして, ここで,複素変数 s の実部 Re (s) をY(0) = y′(0) = 0 (1319) まず、方程式をラプラス変換すると




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2



Excel エクセルでsin Cos Tanを計算する方法 三角関数の計算
111 filas sin 0' 6' 12' 18' 24' 30' 36' 42' 48' 54' 60' cos 1' 2' 3' 90° 0° 0017 0035 0052 0070 0087 0105 0122 0140 0157 0175 ° 3 6 9 1° 0175 0192 09 0227 0244 0262 0279 0297 0314 0332 0349 ° 3 6 9 2° 0349 0366 0384 0401 0419 0436 0454 0471 04 0506 0523 87° 3 6 9 3° 0523 0541 0558 0576 0593 0610 0628X iy cos T i sin T e iT こうすることで、フーリエ展開で だけでは表せない関数も表せる に を加えることは、任意の位相シフト を加えることに相当 kx kx kx A kxB kx Ra kxb kx R kx R kx kx cos cos sin cos sin (cos sin) cos() (coscossinsin) I I I I x y cos Tとsin Tは直交(直交関数 ) 物理数学2三角関数表(2) 角 正弦(sin) 余弦(cos) 正接(tan) 450 455 460 465 064 470 060 475 480 485 490 495



第2章 三角関数




三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ
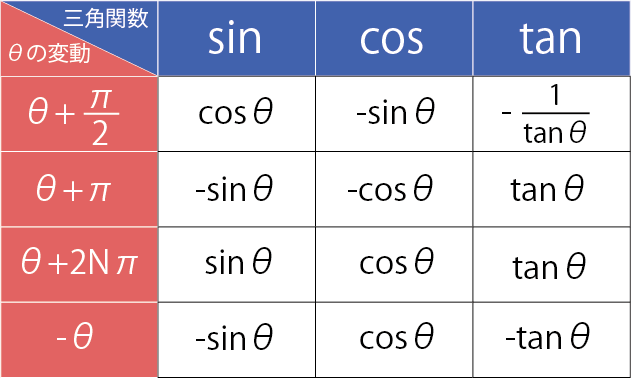
9 0 ∘ 90^{\circ} 9 0 ∘ の奇数倍が絡むものは sin cos \sin\iff \cos sin cos , tan 1 tan \tan\iff\dfrac{1}{\tan} tan tan 1 と変化する 2.符号 θ \theta θ に鋭角を代入して符号を確認します。 公式が成り立つ理由や詳しい解説は 「数学Ⅰ三角比sin cos tanの相互関係と覚え方」 の記事でまとめているので、ぜひ参考にしてください。 数学Ⅰ三角比sin cos tanの相互関係と覚え方 三角比の相互関係 ・ ・ \displaystyle \large { \color {red} { \sin^2 \theta \cos^2 \theta = 1 } } ・ \displaystyle \large { \color {red} { 1 \tan^2 \theta = \frac {1} {\cos^2 \theta} } } 4$$y'=(\sin x)'\cos x\sin x(\cos x)'$$ $$=\cos^2 x\sin^2 x$$ $$=\cos 2x$$




1995 号 ディジタル三角関数発生回路 Astamuse




三角比4 角度が90 以上の三角比はこう考える
三角関数の周期性と対称性から得られる公式 三角関数には、周期性と対称性があります。この性質より、以下の関係式が得られます。 なお、周期性とは、角 θ の大きさに対して、関数(sin θ, cos θ, tan θ)の値が、一定の θ の間隔で繰り返されることを言います。=COS(ラジアン) 角度のtanを返す タンジェント =TAN(ラジアン) 度数とラジアン;ホーム>>カテゴリー分類>>微分>>ラプラス変換>>ラプラス変換表 学生スタッフ作成 初版:09年3月4日,最終更新日: 09年6月23日 ページトップ




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ




三角関数の公式の一覧 Wikipedia
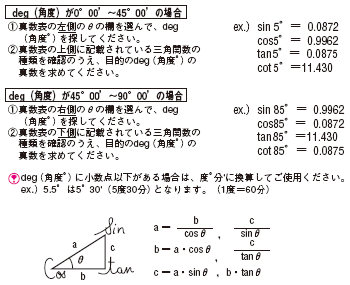
2/7/19 三角関数公式プラス 三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「 加法定理は覚える,他は作る」 というのが,作者おすすめの三角比(sin cos tan)の値の覚え方 その1(表) 当サイト「スマホで学ぶサイト、スマナビング!」では、記事のリクエストや、ご質問・ご意見を募集しています。 三角比の定義• 上の図を見て、対応する辺の数字を当てはめてみましょう。 11図から次の公式が導かれ,これを利用すれば, 180 °~ 270 °の三角関数の値を, 0 °~ 90 °の三角関数に直して求めることができる. 公式 (3) sin (180°θ)=− sin θ cos (180°θ)=− cos θ tan (180°θ)= tan θ 例 sin 1° = sin (180°21°) =− sin 21° = (表より) = − ※三角関数表は0°~90°までの角度に対する正弦,余弦,正接( sin θ, cos θ, tan θ )の値の一覧表として数学書
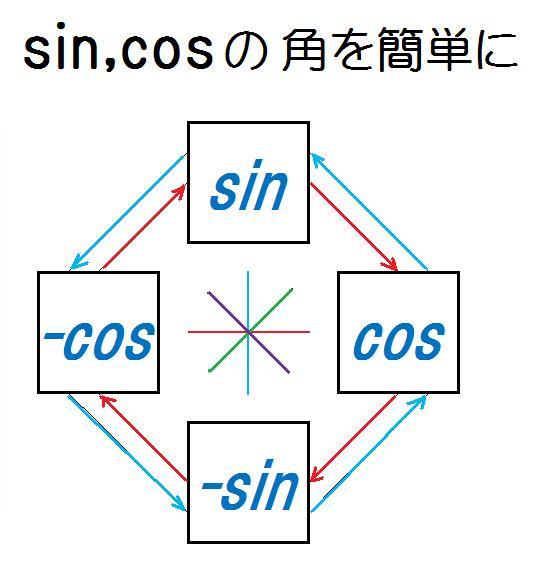



Sin Cos の角を簡単にする図 算数 数学記事



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ
Sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数(度) アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 直角三角形の底辺と傾斜角から斜辺と高さを計算します。 角度と高さから底辺と斜辺を計算 直角三角形の傾斜角と高さから底辺と斜辺を計算します1 ラプラス変換 1 ラプラス変換の基礎問題 問題1 次の関数のラプラス変換を求めよ (1) atb (2) at2 btc (3) eatb (4) cos(ωtθ) (5) sin(ωtθ) (6) cos2 t角度(°) sin(サイン) cos(コサイン) tan(タンジェント) 0 0 1 0 30 1/2 45 1 60 1/2 90 1 0 解なし




三角関数の積分で使う特別な変数変換 t tan X 2 と置換したときのsin cosの導き方 算数数学苦手克服 家庭教師のマスコンサルティング
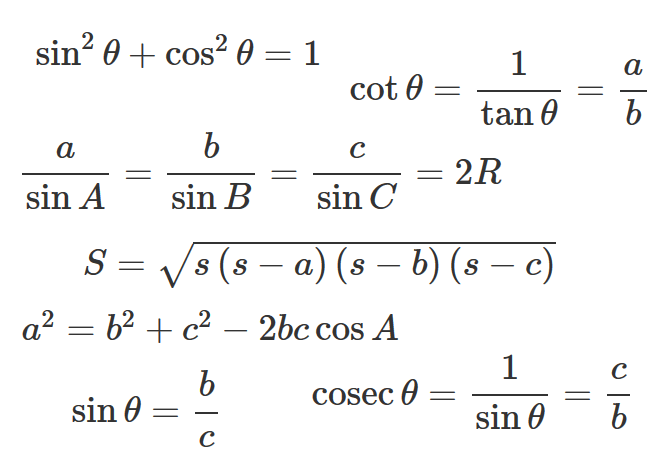



電気数学のお勉強 三角関数
分母にs2 a (a > 0)が現れる場合 この場合は 1 s2a を使って部分分数分解し、逆ラプラス変換してsin( p at);cos( p at)を得るとい う流れになる。5 例)次の初期値問題を考える。 y′′ !2y = 1;2 サインコサイン 変換公式|単位円で考える変換公式 21 \(\sin\left(90^{\circ}θ\right),\cos\left(90^{\circ}θ\right)\) 22 \(\sin\left(180^{\circ}θ\right),\cos\left(180^{\circ}θ\right)\) 23 \(\sin(θ),\cos(θ)\) 24 \(\sin(90^{\circ}θ)、\sin(90^{\circ}θ)\) 25 \(\sin(180^{\circ}θ)、\cos(180^{\circ}θ)\)ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 θ sin 2 θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる: sin θ = ± 1 − cos 2 θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}




ラプラス変換をわかりやすく 変換表を知ろう 物理講師デルタ先生の部屋




三角関数の公式の一覧 Wikipedia
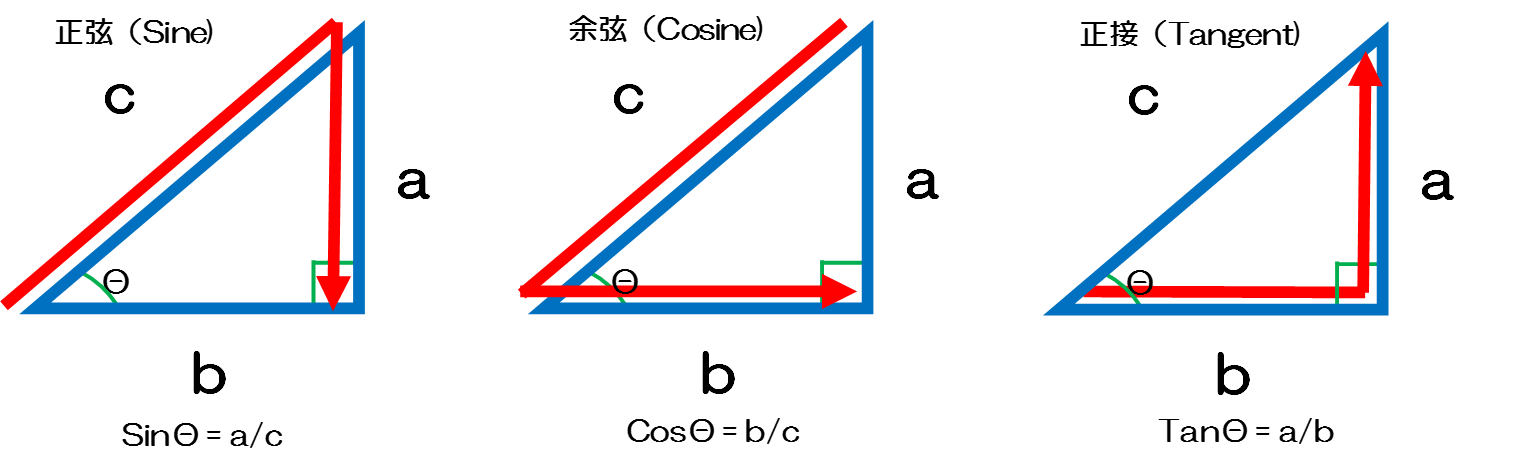
19/2/21 三角比とは? 三角比とは、長さの測量のために生み出された概念で、直角三角形の \(\bf{2}\) 辺の比を角度を使って表したものです。 直角三角形の場合、\(1\) つの鋭角の大きさを決めるとすべての角の大きさが決まり、辺の比も決まります。



三角関数表 Pukiwiki




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




画像の周波数特性の基礎 三角関数の基本特性



三角関数の公式 Sin Cos Tan と覚え方




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita




日本人全員に三角関数を教える必要がない2つの理由 ハフポスト




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2




三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook




三角比の表 Sin Cos Tan 30 45 60 1 の値 Irohabook



1



正弦波の位相を調べる問題で Cosからsinに変換する時 P 2 Yahoo 知恵袋




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ




1995 号 ディジタル三角関数発生回路 Astamuse




三角関数 の基本的な定理とその有用性を再確認してみませんか その2 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所




P1 Sinのz変換 Chapter6




高校数学 三角関数 公式一覧 変換 倍角 半角 3倍角 合成関数 学校よりわかりやすいサイト




三角関数の公式の一覧 Wikipedia



Http Www Material Tohoku Ac Jp Hyoka R1 Math2 Chap2 Pdf



三角関数 初等数学 基礎からの数学入門




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学
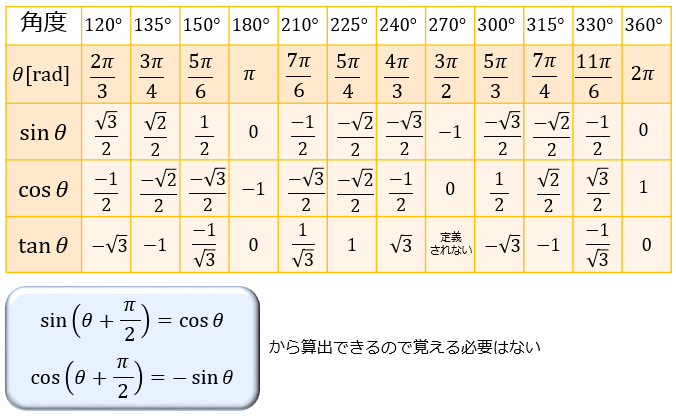



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ




三角関数の公式の一覧 Wikipedia



数学 三角関数 Abs Pi Sinなど の使い方 Excel関数




三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook
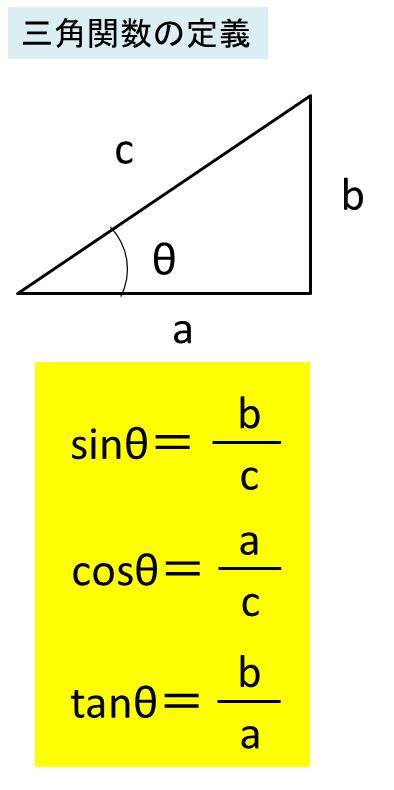



Excel エクセルでsin Cos Tanを計算する方法 三角関数の計算




Excel エクセルでsin Cos Tanを計算する方法 三角関数の計算
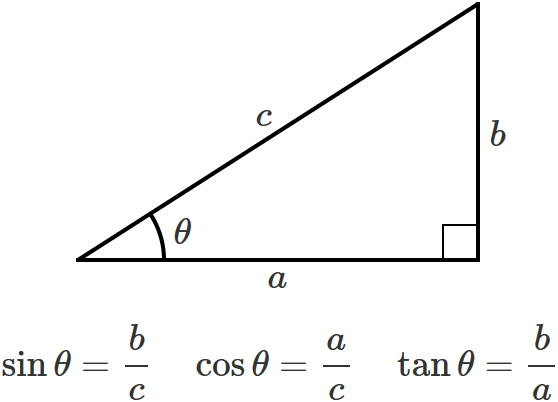



電気数学のお勉強 三角関数




三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




Sin Cos Tanの超重要な4つの関係式をシンプルに




6 ラプラス変換 Ppt Download



三角比 三角関数を総まとめ 定義や各種公式 重要記事一覧 受験辞典




和積 積和 変換公式 おいしい数学



Excelで三角関数の計算が出来る関数を覚えよう Sin Cos Tan 関数の使用 パソコンスキルと資格のscワンポイント講座




ラプラス変換表と証明まとめ ばたぱら



三角関数表 Pukiwiki



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数




答えにマイナスがつくのとつかないのの違いがわかりま Clear




ラプラス変換をわかりやすく 変換表を知ろう 物理講師デルタ先生の部屋



三角比の表と面積公式 正弦定理 余弦定理を一記事で解説
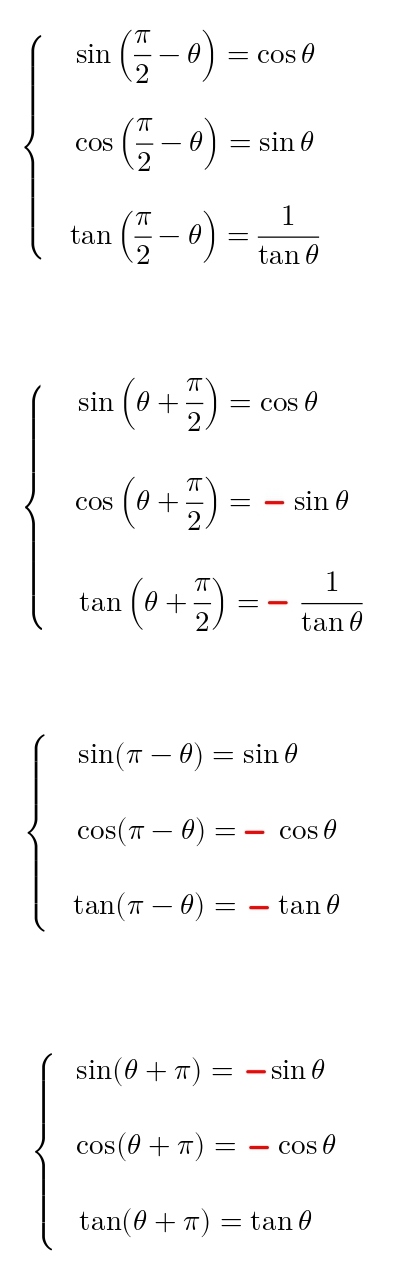



高校数学 三角関数 公式一覧 変換 倍角 半角 3倍角 合成関数 学校よりわかりやすいサイト



第2章 三角関数




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ



ラジアン Rad 弧度法とは 定義 角度との変換や計算 受験辞典



三角関数の基礎 必ず覚えておかなくてはならない5つの性質とは 高校生向け受験応援メディア 受験のミカタ




数学 三角比 Sin Cos Tanの変換公式と覚え方 理系ラボ




弧度法とは 度数法との違いと表 求め方 理系ラボ




三角関数の知識 やさしい電気回路




三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要




Sin サイン とcos コサイン との関係



1




Sin Cos Tan 高校生 数学のノート Clear
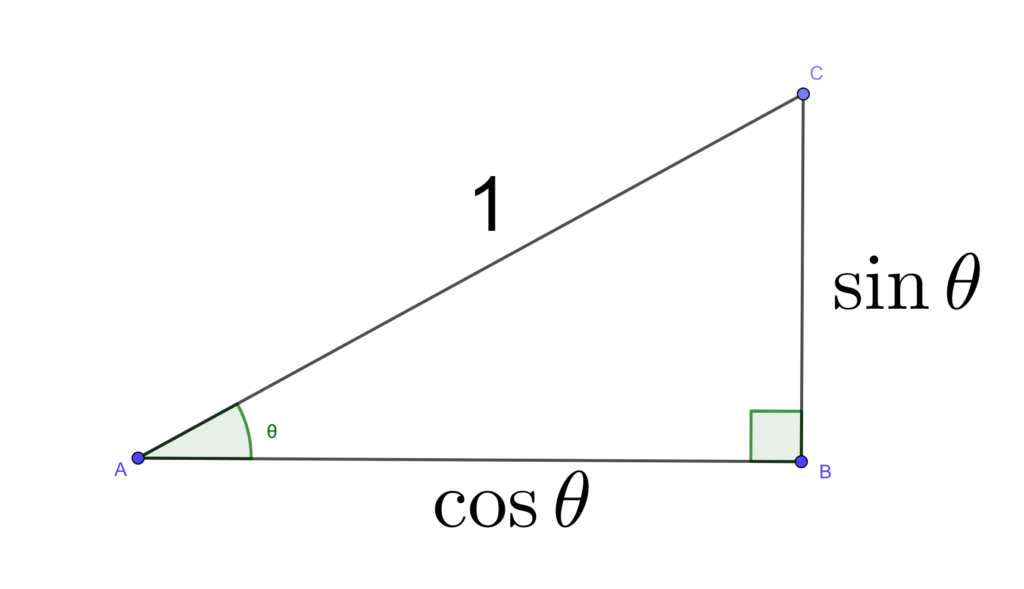



忘れても大丈夫 サインコサインの変換公式 覚え方とコツ 単位円を描こう 青春マスマティック




三角関数 積和の公式 和積の公式 忘れていたら即クリック 高校生向け受験応援メディア 受験のミカタ



Www Kyokyo U Ac Jp Cece 2 3 Pdf
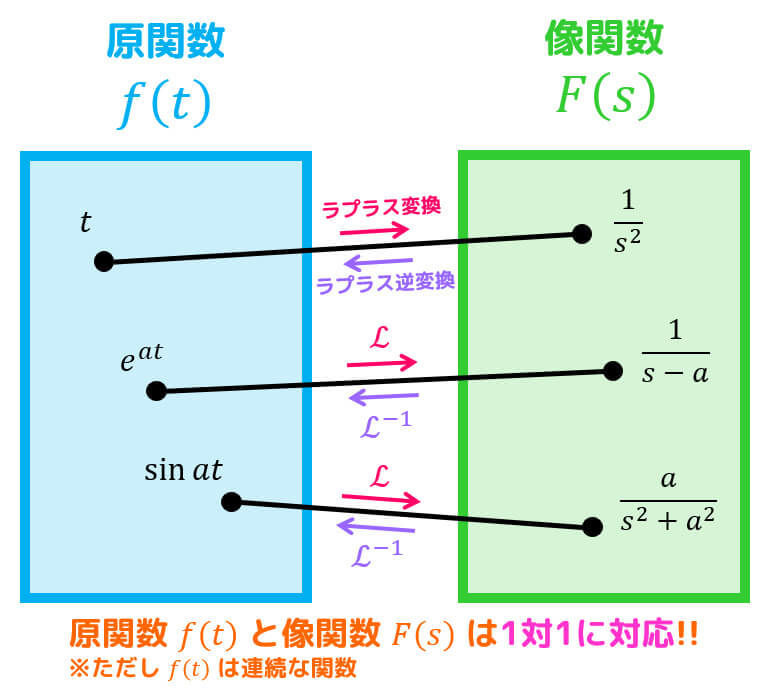



うさぎでもわかる微分方程式 Part14 ラプラス変換のいろは 工業大学生ももやまのうさぎ塾




三角関数の公式の一覧 Wikipedia



三角関数表 Pukiwiki




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学



フーリエ変換3




三角関数の知識 やさしい電気回路



3




三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook
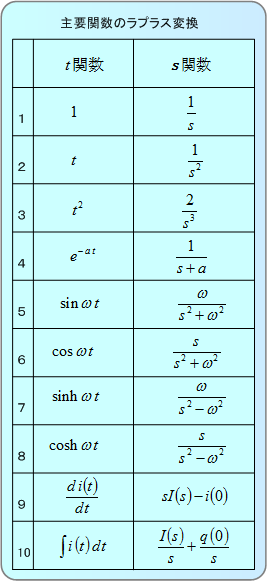



ラプラス変換とその使い方1 基礎編 ラプラス変換とは何か 変換の基礎事項は 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
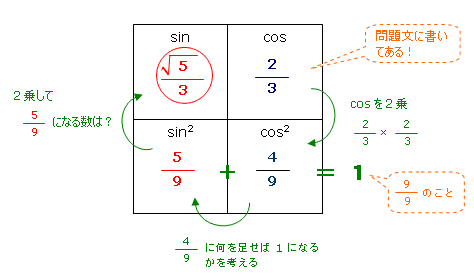



Sin サイン とcos コサイン との関係
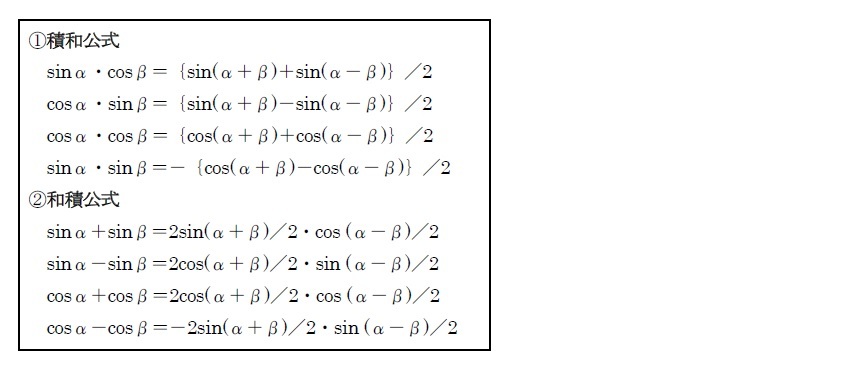



三角関数 の基本的な定理とその有用性を再確認してみませんか その2 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所



数学 三角関数 Abs Pi Sinなど の使い方 Excel関数



三角関数表 Pukiwiki




三角関数の知識 やさしい電気回路




三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ
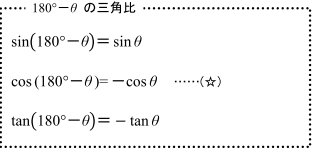



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座




Excelの三角関数 Sin Cos Tan の具体的な使い方と注意点 サインコサインタンジェント わえなび ワード エクセル問題集




三角関数の知識 やさしい電気回路



3




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




ラプラス変換をわかりやすく 変換表を知ろう 物理講師デルタ先生の部屋
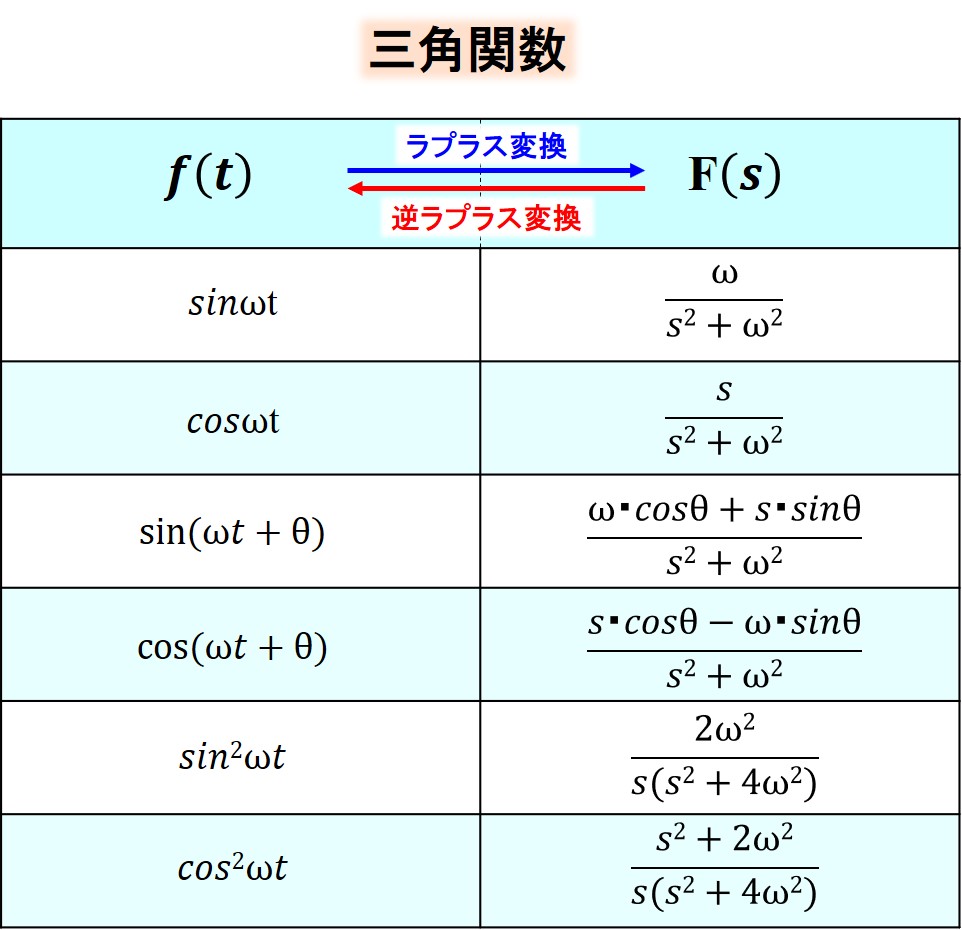



ラプラス変換をわかりやすく 変換表を知ろう 物理講師デルタ先生の部屋
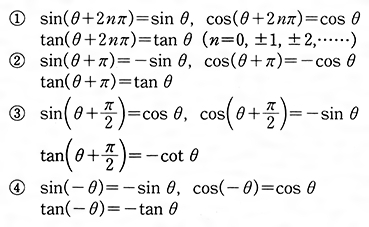



三角関数とは コトバンク




三角関数 の基本的な定理とその有用性を再確認してみませんか その2 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所
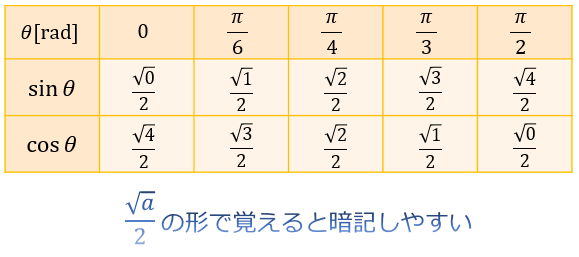



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ



0 件のコメント:
コメントを投稿